Word Vectors with tidy data principles
By Julia Silge
October 30, 2017
Last week I saw Chris Moody’s post on the Stitch Fix blog about calculating word vectors from a corpus of text using word counts and matrix factorization, and I was so excited! This blog post illustrates how to implement that approach to find word vector representations in R using tidy data principles and sparse matrices.
Word vectors, or word embeddings, are typically calculated using neural networks; that is what word2vec is. (GloVe embeddings are trained a little differently than word2vec.) By contrast, the approach from Chris’s post that I’m implementing here uses only counting and some linear algebra. Deep learning is great, but I am super excited about this approach because it allows practitioners to find word vectors for their own collections of text (no need to rely on pre-trained vectors) using familiar techniques that are not difficult to understand. And it doesn’t take too long computationally!
Getting some data
Let’s download half a million observations from… the Hacker News corpus.
I know, right? But it’s the dataset that Chris uses in his blog post and it gives me an opportunity to use the bigrquery package for the first time.
library(bigrquery)
library(tidyverse)
project <- "my-first-project-184003"
sql <- "#legacySQL
SELECT
stories.title AS title,
stories.text AS text
FROM
[bigquery-public-data:hacker_news.full] AS stories
WHERE
stories.deleted IS NULL
LIMIT
500000"
hacker_news_raw <- query_exec(sql, project = project, max_pages = Inf)Next, let’s clean this text up to take care of some of the messy ways it has gotten encoded.
library(stringr)
hacker_news_text <- hacker_news_raw %>%
as_tibble() %>%
mutate(title = na_if(title, ""),
text = coalesce(title, text)) %>%
select(-title) %>%
mutate(text = str_replace_all(text, ""|/", "'"), ## hex encoding
text = str_replace_all(text, "/", "/"), ## more hex
text = str_replace_all(text, "<a(.*?)>", " "), ## links
text = str_replace_all(text, ">|<", " "), ## html yuck
text = str_replace_all(text, "<[^>]*>", " "), ## mmmmm, more html yuck
postID = row_number())Unigram probabilities
First, let’s calculate the unigram probabilities, how often we see each word in this corpus. This is straightforward using unnest_tokens() from the tidytext package and then just count() and mutate() from dplyr.
library(tidytext)
unigram_probs <- hacker_news_text %>%
unnest_tokens(word, text) %>%
count(word, sort = TRUE) %>%
mutate(p = n / sum(n))
unigram_probs## # A tibble: 314,615 x 3
## word n p
## <chr> <int> <dbl>
## 1 the 1101051 0.04059959
## 2 to 761660 0.02808506
## 3 a 669142 0.02467360
## 4 of 541939 0.01998318
## 5 and 532594 0.01963860
## 6 i 464917 0.01714311
## 7 x27 437330 0.01612588
## 8 is 431849 0.01592378
## 9 that 429755 0.01584657
## 10 it 402667 0.01484774
## # ... with 314,605 more rowsSkipgram probabilities
Next, we need to calculate the skipgram probabilities, how often we find each word near each other word. We do this by defining a fixed-size moving window that centers around each word. Do we see word1 and word2 together within this window? I take the approach here of using unnest_tokens() once with token = "ngrams" to find all the windows I need, then using unnest_tokens() again to tidy these n-grams. After that, I can use pairwise_count() from the widyr package to count up cooccuring pairs within each n-gram/sliding window.
I’m not sure what the ideal value for window size is here for the skipgrams. This value determines the sliding window that we move through the text, counting up bigrams that we find within the window. When this window is bigger, the process of counting skipgrams takes longer, obviously. I experimented a bit and windows of 8 words seem to work pretty well. Probably more work needed here! I’d be happy to be pointed to more resources on this topic.
Finding all the skipgrams is a computationally expensive part of this process. Not something that just runs instantly!
library(widyr)
tidy_skipgrams <- hacker_news_text %>%
unnest_tokens(ngram, text, token = "ngrams", n = 8) %>%
mutate(ngramID = row_number()) %>%
unite(skipgramID, postID, ngramID) %>%
unnest_tokens(word, ngram)
tidy_skipgrams## # A tibble: 190,151,488 x 2
## skipgramID word
## <chr> <chr>
## 1 1_1 i
## 2 1_1 bet
## 3 1_1 taking
## 4 1_1 a
## 5 1_1 few
## 6 1_1 months
## 7 1_1 off
## 8 1_1 from
## 9 1_2 bet
## 10 1_2 taking
## # ... with 190,151,478 more rowsskipgram_probs <- tidy_skipgrams %>%
pairwise_count(word, skipgramID, diag = TRUE, sort = TRUE) %>%
mutate(p = n / sum(n))Normalized skipgram probability
We now know how often words occur on their own, and how often words occur together with other words. We can calculate which words occurred together more often than expected based on how often they occurred on their own. When this number is high (greater than 1), the two words are associated with each other, likely to occur together. When this number is low (less than 1), the two words are not associated with each other, unlikely to occur together.
normalized_prob <- skipgram_probs %>%
filter(n > 20) %>%
rename(word1 = item1, word2 = item2) %>%
left_join(unigram_probs %>%
select(word1 = word, p1 = p),
by = "word1") %>%
left_join(unigram_probs %>%
select(word2 = word, p2 = p),
by = "word2") %>%
mutate(p_together = p / p1 / p2)What are the words most associated with Facebook on Hacker News?
normalized_prob %>%
filter(word1 == "facebook") %>%
arrange(-p_together)## # A tibble: 1,767 x 7
## word1 word2 n p p1 p2 p_together
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 facebook facebook 54505 3.737944e-05 0.0003310502 3.310502e-04 341.07126
## 2 facebook messenger 364 2.496306e-07 0.0003310502 1.098830e-05 68.62360
## 3 facebook statuses 40 2.743194e-08 0.0003310502 1.474940e-06 56.18086
## 4 facebook zuckerburg 23 1.577336e-08 0.0003310502 8.480903e-07 56.18086
## 5 facebook myspace 327 2.242561e-07 0.0003310502 1.290572e-05 52.48898
## 6 facebook newsfeed 32 2.194555e-08 0.0003310502 1.327446e-06 49.93854
## 7 facebook hiphop 29 1.988815e-08 0.0003310502 1.438066e-06 41.77551
## 8 facebook mashable.com 25 1.714496e-08 0.0003310502 1.253699e-06 41.30946
## 9 facebook gtalk 22 1.508757e-08 0.0003310502 1.216825e-06 37.45391
## 10 facebook www.facebook.com 47 3.223253e-08 0.0003310502 2.765512e-06 35.20667
## # ... with 1,757 more rowsWhat about the programming language Scala?
normalized_prob %>%
filter(word1 == "scala") %>%
arrange(-p_together)## # A tibble: 453 x 7
## word1 word2 n p p1 p2 p_together
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 scala scala 9418 6.458850e-06 5.394592e-05 5.394592e-05 2219.41246
## 2 scala odersky 54 3.703312e-08 5.394592e-05 1.216825e-06 564.16154
## 3 scala sbt 36 2.468874e-08 5.394592e-05 1.401193e-06 326.61984
## 4 scala akka 74 5.074908e-08 5.394592e-05 2.913006e-06 322.94479
## 5 scala groovy 88 6.035026e-08 5.394592e-05 5.494150e-06 203.61983
## 6 scala mu 23 1.577336e-08 5.394592e-05 1.769928e-06 165.20008
## 7 scala kotlin 88 6.035026e-08 5.394592e-05 7.448445e-06 150.19482
## 8 scala constructors 23 1.577336e-08 5.394592e-05 2.728638e-06 107.15681
## 9 scala clojure 475 3.257543e-07 5.394592e-05 5.678518e-05 106.33997
## 10 scala idiomatic 53 3.634732e-08 5.394592e-05 7.337825e-06 91.82194
## # ... with 443 more rowsLooks good!
Cast to a sparse matrix
We want to do matrix factorization, so we should probably make a matrix. We can use cast_sparse() from the tidytext package to transform our tidy data frame to a matrix.
pmi_matrix <- normalized_prob %>%
mutate(pmi = log10(p_together)) %>%
cast_sparse(word1, word2, pmi)What is the type of this object?
class(pmi_matrix)## [1] "dgCMatrix"
## attr(,"package")
## [1] "Matrix"The dgCMatrix class is a class of sparse numeric matrices in R. Text data like this represented in matrix form usually has lots and lots of zeroes, so we want to make use of sparse data structures to save us time and memory and all that.
Reduce the matrix dimensionality
We want to get information out of this giant matrix in a more useful form, so it’s time for singular value decomposition. Since we have a sparse matrix, we don’t want to use base R’s svd function, which casts the input to a plain old matrix (not sparse) first thing. Instead we will use the fast SVD algorithm for sparse matrices in the irlba package.
library(irlba)
pmi_svd <- irlba(pmi_matrix, 256, maxit = 1e3)The number 256 here means that we are finding 256-dimensional vectors for the words. This is another thing that I am not sure exactly what the best number is, but it will be easy to experiment with. Doing the matrix factorization is another part of this process that is a bit time intensive, but certainly not slow compared to training word2vec on a big corpus. In my experimenting here, it takes less time than counting up the skipgrams.
Once we have the singular value decomposition, we can get out the word vectors! Let’s set some row names, using our input, so we can find out what is what.
word_vectors <- pmi_svd$u
rownames(word_vectors) <- rownames(pmi_matrix)Now we can search our matrix of word vectors to find synonyms. I want to get back to a tidy data structure at this point, so I’ll write a new little function for tidying.
library(broom)
search_synonyms <- function(word_vectors, selected_vector) {
similarities <- word_vectors %*% selected_vector %>%
tidy() %>%
as_tibble() %>%
rename(token = .rownames,
similarity = unrowname.x.)
similarities %>%
arrange(-similarity)
}
facebook <- search_synonyms(word_vectors, word_vectors["facebook",])
facebook## # A tibble: 68,664 x 2
## token similarity
## <chr> <dbl>
## 1 facebook 0.07622816
## 2 twitter 0.05477529
## 3 google 0.04833987
## 4 social 0.04367801
## 5 fb 0.03597795
## 6 account 0.03304327
## 7 instagram 0.02955428
## 8 users 0.02581671
## 9 photos 0.02502522
## 10 friends 0.02412458
## # ... with 68,654 more rowshaskell <- search_synonyms(word_vectors, word_vectors["haskell",])
haskell## # A tibble: 68,664 x 2
## token similarity
## <chr> <dbl>
## 1 haskell 0.04100067
## 2 lisp 0.03796378
## 3 languages 0.03710574
## 4 language 0.03176253
## 5 functional 0.03022514
## 6 programming 0.02743172
## 7 scala 0.02667198
## 8 clojure 0.02652761
## 9 python 0.02462822
## 10 erlang 0.02452040
## # ... with 68,654 more rowsThat’s… pretty darn amazing. Let’s visualize the most similar words vector to Facebook and Haskell from this dataset of Hacker News posts.
facebook %>%
mutate(selected = "facebook") %>%
bind_rows(haskell %>%
mutate(selected = "haskell")) %>%
group_by(selected) %>%
top_n(15, similarity) %>%
ungroup %>%
mutate(token = reorder(token, similarity)) %>%
ggplot(aes(token, similarity, fill = selected)) +
geom_col(show.legend = FALSE) +
facet_wrap(~selected, scales = "free") +
coord_flip() +
theme(strip.text=element_text(hjust=0, family="Roboto-Bold", size=12)) +
scale_y_continuous(expand = c(0,0)) +
labs(x = NULL, title = "What word vectors are most similar to Facebook or Haskell?",
subtitle = "Based on the Hacker News corpus, calculated using counts and matrix factorization")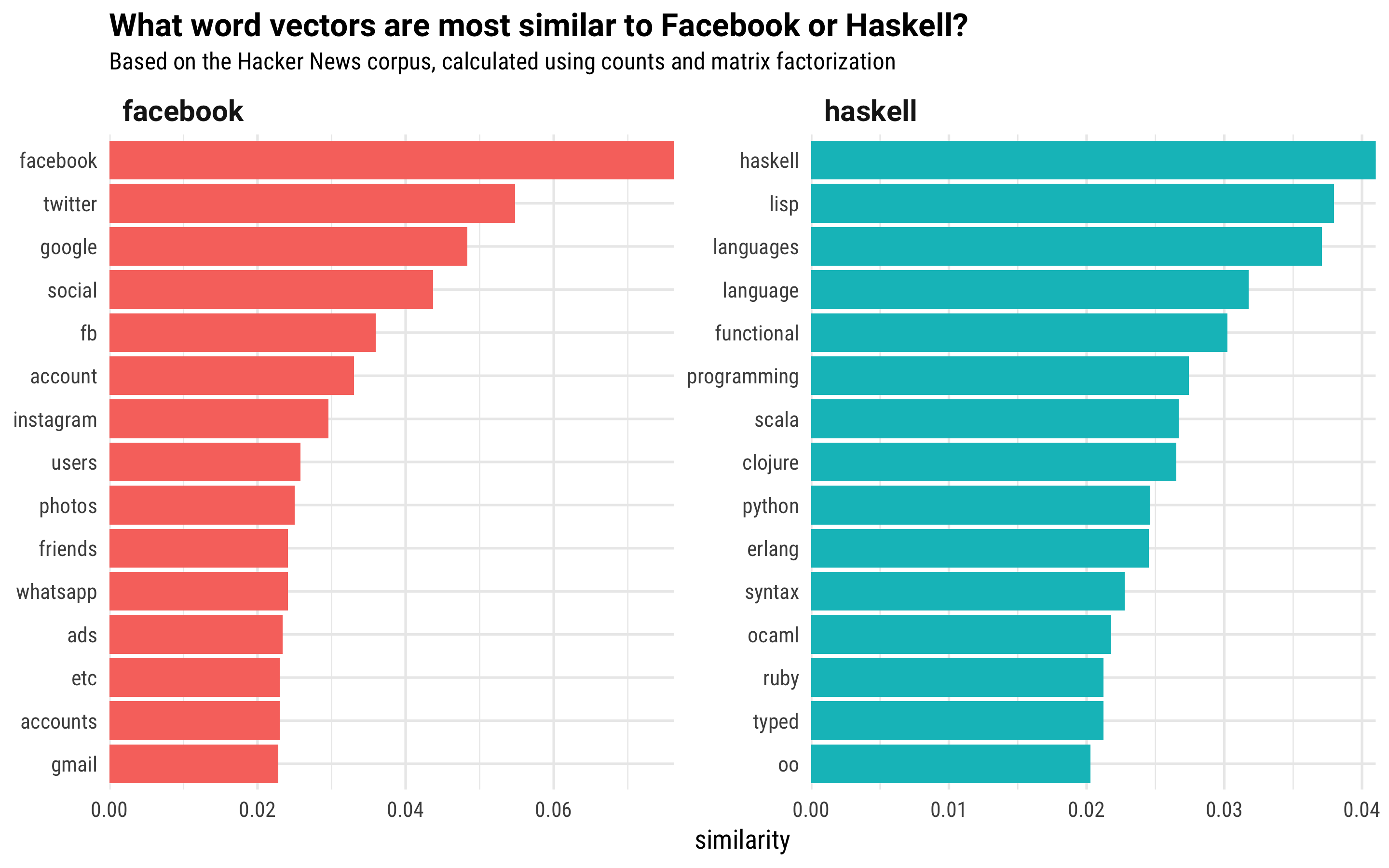
We can also do the familiar WORD MATH that is so fun with the output of word2vec; you have probably seen examples such as King - Man + Woman = Queen and such. We can just add and subtract our word vectors, and then search the matrix we built!
If the iPhone is an important product associated with Apple, as discussed on Hacker News, what is an important product associated with Microsoft?
mystery_product <- word_vectors["iphone",] - word_vectors["apple",] + word_vectors["microsoft",]
search_synonyms(word_vectors, mystery_product)## # A tibble: 68,664 x 2
## token similarity
## <chr> <dbl>
## 1 windows 0.03861497
## 2 phone 0.02818951
## 3 iphone 0.02444977
## 4 mobile 0.02427238
## 5 android 0.02321326
## 6 microsoft 0.02233597
## 7 ios 0.02138345
## 8 office 0.02000720
## 9 7 0.01997405
## 10 8 0.01970687
## # ... with 68,654 more rowsWe even see some mobile phone and Android terms in this list, below Windows.
What about an important product associated with Google?
mystery_product <- word_vectors["iphone",] - word_vectors["apple",] + word_vectors["google",]
search_synonyms(word_vectors, mystery_product)## # A tibble: 68,664 x 2
## token similarity
## <chr> <dbl>
## 1 google 0.10194467
## 2 search 0.05937512
## 3 phone 0.03947618
## 4 app 0.03716764
## 5 engine 0.03590006
## 6 facebook 0.03513982
## 7 android 0.03289141
## 8 q 0.02998453
## 9 gmail 0.02980005
## 10 using 0.02944208
## # ... with 68,654 more rowsGoogle itself is at the top of the list, which is something that often happens to me when I try this word vector arithmetic no matter how I train them (usually one of the positive vectors in the “equation”). Does anyone know what that means? Anyway, “search”, is next on the list.
mystery_product <- word_vectors["iphone",] - word_vectors["apple",] + word_vectors["amazon",]
search_synonyms(word_vectors, mystery_product)## # A tibble: 68,664 x 2
## token similarity
## <chr> <dbl>
## 1 amazon 0.04757609
## 2 aws 0.04389115
## 3 s3 0.03356846
## 4 book 0.03273032
## 5 ec2 0.03151250
## 6 cloud 0.03083856
## 7 books 0.03008677
## 8 iphone 0.02749843
## 9 storage 0.02549876
## 10 kindle 0.02505824
## # ... with 68,654 more rowsFor Amazon, we get AWS, S3, and EC2, as well as book. Nice!
The End
I am so excited about this approach! Like Chris said in his blog post, for all the applications in the kind of work I do (non-academic, industry NLP) these type of word vectors will work great. No need for neural networks! This approach is still not lightning fast (I have to sit and wait for parts of it to run) but I can easily implement it with the tools I am familiar with. I would imagine there are vast swaths of data science practitioners for whom this is also true. I am considering the idea of bundling some of these types of functions up into an R package, and Dave has just built a pairwise_pmi() function in the development version of widyr that simplifies this approach even more. Tidy word vectors, perhaps? Maybe I’ll also look into the higher rank extension of this technique to get at word and document vectors!
Let me know if you have feedback or questions.